Is tituto Profess ionale di Stato pe r l’Indus tria e l’Artigianato
“CAVOUR-MARCONI”
Loc. Piscille–Via Assisana, 40/d-06154 PERUGIA– Tel. 075/5838322 Fax 075/32371
e-mail: i p s i a p g @ t i n . i t - sito internet: w w w . i p s i a p g . i t
Modulo N.4 di recupero relativo al sistema trifase N.4
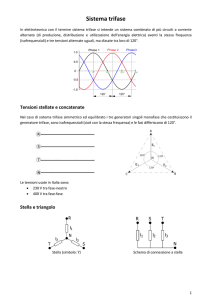
Sistemi trifase: generalità
I sistemi trifase si inquadrano nella teoria generale degli n-poli, dove i “morsetti” sono n>2
(per n=2 si ritorna ai bipoli).
Caratteristiche dei sistemi di connessione di tripoli attraverso tre connessioni (linee o fasi12-3 [RST nella nomenclatura ENEL], da cui la dizione di sistema trifase).
1) Il sistema trifase è equivalente a tre sistemi monofasi
2) Si individuano immediatamente tre correnti di linea I1,I2,I3 e tre tensioni
concatenate V12,V23,V31.
3) Le tre correnti di linea sono tra di loro dipendenti (come le tre tensioni
concatenate). La loro somma è nulla.
4) Sul piano complesso (piano di Gauss), le tre grandezze danno luogo ad una figura
chiusa (triangolo in genere scaleno).
5) Il generatore trifase può essere rappresentato con tre generatori indipendenti di
tensione stellati, ossia avente un morsetto collegato ad un unico punto Og detto
centro stella del generatore.
6) Anche l’utilizzatore può essere rappresentato da una stella di impedenze di
centrostella Ou.
7) Se non c’è collegamento ulteriore tra i due centri stella il sistema si dirà puro. In
questo caso la tensione tra i due centri stella è in genere diversa da zero e può
essere calcolata attraverso la formula di Millman, a sua volta ricavata applicando il
teorema di Norton.
8) Le correnti di linea si ricavano di conseguenza. Un ulteriore collegamento può
essere realizzato tra i due centri stella attraverso un conduttore (conduttore 0 o
neutro) che qui consideriamo ideale. In presenza del neutro la tensione tra i centri
stella è nulla e le correnti dipendono dal generatore e dall’impedenza della singola
linea (è la soluzione adottata in campo civile per l’utilizzazione dell’energia elettrica
in bassa tensione, per avere carichi in funzionamento indipendente).
9) Nel collegamento senza neutro il sistema si dice puro, in presenza del neutro si
dice spurio.
10) Se le tensioni dei generatori sono simmetriche (uguale valore efficace e sfasamento
mutuo di 120°) e le impedenze sono uguali (carico equilibrato) la tensione tra i
centri stella è nulla anche nei sistemi puri.
I principali vantaggi dei sistemi trifase sono:
a) a parità di potenza media assorbita dall’utilizzatore, nel sistema simmetrico ed
equilibrato si risparmia il 50% dei conduttori (nei sistemi spuri il 33%); la potenza
istantanea assorbita da un sistema trifase simmetrico ed equilibrato risulta essere pari alla
potenza media; vengono così evitati i gravosi inconvenienti connessi con la potenza
fluttuante.
b) miglior rendimento delle macchine come utilizzatori trifase, (ad esempio motore
asincroni trifase) rispetto alle macchine monofasi;
c) nel caso del trifase spurio, cioè con neutro, si hanno a disposizione due livelli di
tensione, quelle di fase e quelle concatenate;
d) si risparmia sul calibro dei dispositivi di manovra e protezione, interruttori e fusibili,
poiché a pari potenza le correnti sono ridotte nel trifase.
Cosa si può fare con una alimentazione monofase
Alimentare impianti domestici o similari (uffici, negozi e terziario in
generale).
Alimentare piccoli laboratori artigianali fino a 10 kW di potenza.
Alimentare apparecchiature che per loro natura sono monofase
(lampade, computer, macchine monofasi in genere e motori universali in
particolare).
Si utilizzano solo due conduttori (in certe applicazioni si può impiegarne anche solo uno,
Vantaggi
esempio ferrovie progetto TAV=treno alta velocità, alimentazione monofase a 15 kV e 50 Hz, tra conduttore
sospeso e ritorno via rotaia. Tutte le altre linee ferroviarie sono alimentate in corrente continua a 3000 Volt).
Il livello di tensione tra i due conduttori non è molto elevato (230 V a 50
Hz di frequenza).
Si può utilizzare il trasformatore monofase per cambiare il livello di
tensione (ad esempio per ridurla a 48 V o 24 V o 12 V).
Si può passare alla corrente continua con sistemi di conversione
semplici, usando un trasformatore monofase la cui uscita sia inviata ad
un ponte di Graetz monofase.
Si può utilizzare l’inverter con alimentazione monofase ed uscita trifase a
frequenza qualsiasi, variandone la frequenza.
Difficoltà
Alcune macchine elettriche monofase hanno basso rendimento (motori
asincroni monofase).
In monofase le correnti sono elevate, se confrontate con quelle degli
impianti trifase che alimentino lo stesso carico (tre volte maggiori).
In monofase le cadute di tensione sono più alte, il valore della corrente
circolante risulta maggiore e quindi le linee devono essere più corte.
In monofase, se uno dei due conduttori si interrompe per un guasto alla
linea, si verifica un blocco nel funzionamento delle apparecchiature
(esempio: i motori si fermano e le lampade si spengono).
Le forme che si ottengono in uscita da un sistema di conversione
monofase presentano più componenti armoniche rispetto ad un
impianto trifase, inoltre il sistema presenta ridotto rendimento.
I componenti di manovra e protezione del sistema (interruttori, fusibili,
relè) vanno scelti con calibro più alto rispetto a quelli utilizzati nei
sistemi trifase, sono quindi più costosi.
Cosa si può fare con una alimentazione trifase
In trifase si hanno a disposizione due livelli di tensione: 230 V fase –
neutro e 400 V fase – fase.
In trifase si usano conduttori con sezione minore rispetto all’impianto
monofase, poiché la corrente risulta minore (in trifase, a parità di
potenza dell’utenza finale, la corrente è un terzo rispetto alla corrente in
monofase).
In trifase si la possibilità di realizzare linee più lunghe a pari caduta di
tensione, per le stesse ragioni di sopra.
In trifase si usano macchine elettriche trifase, che, a parità di potenza,
hanno un rendimento più alto di quelle monofase.
A partire dal sistema trifase si può ottenere una alimentazione in
continua (con sistema di conversione a ponte di Graetz, con sei diodi)
con maggior rendimento rispetto alla conversione in continua a partire
da un sistema monofase, migliorando anche la forma d’onda (che
diventa più pulita) in uscita.
In trifase si ,igliora l’equilibrio del carico, poiché può essere ripartito in
forma ottimale sulle tre fasi (si pensi ad esempio ad un grande impianto
di illuminazione).
Al limite si potrebbe avere una uscita trasformatorica a tensione ancora
più alta per esempio 660 V, questo ridurrebbe ulteriormente la corrente
circolante (questo però potrebbe creare qualche problema per la
sicurezza dell’impianto).
Alcune macchine hanno l’alimentazione solo trifase, per esempio i grandi
server (cioè i computer di rete).
In presenza di interruzione di un conduttore,
1) in monofase assolutamente non si può continuare a lavorare, per esempio
con un motore,
2) in impianto trifase, anche in presenza di interruzione, su di un conduttore, si
può continuare a lavorare e comunque si ha a disposizione ancora tensione
sulle due fasi sane.
In trifase i dispositivi di manovra e protezione quali: interruttori
automatici, teleruttori, commutatori semirotativi a camme, valvole
fusibili, ecc., vanno dimensionati per un valore di corrente più basso a
pari potenza rispetto alle utenze monofasi.
Si può utilizzare una macchina speciale, che realizza il cambio del
numero delle fasi, da monofase a trifase, che per modeste potenze
risulta portatile e quindi utilizzabile dovunque.
In trifase si utilizza, come in monofase, l’inverter, che consente di
variare a piacere il valore della frequenza delle tensioni in uscita (campo
di variazione compreso nei limiti: 2 – 120 Hz).
In trifase si impiegano sistemi di avviamento di tipo elettronico per
motori asincroni trifase, questi sistemi che migliorano consistentemente
il comportamento del motore durante il transitorio (ad esempio
riducendone la corrente di spunto).
In trifase è molto semplice e poco costoso, cambiare il senso di
rotazione nelle macchine, come motori asincroni trifase (cambio di due
fasi su tre).
Nelle macchine elettriche trifase non si utilizzano collettori e quindi non
ci sono contatti striscianti (solo il motore asincrono trifase con rotore
avvolto ha contatti striscianti).
Si può variare la velocità di rotazione del rotore dei motori trifase con
sistemi semplici (Dahalander).
Si possono piazzare due avvolgimenti nelle stesse cave di statore per
produrre due distinte velocità nei motori asincroni trifase.
Nella fase di produzione dell’energia elettrica si può impiegare il
generatore sincrono trifase (alternatore), macchina ad altissimo
rendimento.
Si può passare in forma semplice e poco costosa ad una alimentazione
monofase, basta derivare un conduttore da una delle tre fasi e l’altro dal
centro stella del sistema, questo conduttore si chiama, conduttore di
neutro o semplicemente neutro, può essere collegato a terra oppure
isolato da terra, i tre sistemi vengono indicati con le sigle TT, TN, IT.
Non è invece altrettanto facile passare da un sistema monofase ad uno
trifase, comunque ci sono due possibilità: la prima è quella di utilizzare
un inverter con ingresso monofase ed uscita trifase, il più economico
disponibile costa € 300.00; la seconda sfrutta le qualità del motore
asincrono trifase, il sistema costa molto meno, ma non consente
controlli in frequenza in forma continua.
Si possono impiegare i trasformatori speciali, macchine comunque a
buon rendimento, trasformatore del numero delle fasi, trasformatore a
tre avvolgimenti, autotrasformatori, surdevoltori, ecc…
Si possono utilizzare i motori asincroni come macchine speciali, si
ricorda l’utilizzazione da sfasatore, si può regolare opportunamente la
fase di una terna di tensioni in uscita.
Si impiega la macchina sincrona trifase come motore, in condizioni di
sovreccitazione, essa si comporta come una terna di condensatori,
questa funzione viene denominata con la frase, compensatore rotante,
regolando opportunamente l’eccitazione si modifica il valore della
potenza di tipo reattivo scambiata con il carico.
Nel caso di trasporto a lunga distanza di ingenti quantità di potenza a
conduttori nudi, risulta più conveniente l’utilizzo del sistema trifase,
come peso complessivo del materiale conduttore, rispetto agli altri
possibili, cioè sistema monofase e sistema in corrente continua, purché
in fattore di potenza del sistema trifase venga mantenuto superiore al
limite 0.866.
Il sistema trifase è di utilizzazione comune poiché, secondo il principio di
Galileo Ferraris, al traferro delle macchine asincrone si localizza un
campo magnetico rotante puro.
Nella distribuzione in BT si usa il sistema trifase a quattro conduttori (tre
di fase più il conduttore neutro), anziché il trifase quello a tre
conduttori, perchè a pari potenza persa in linea, i conduttori del primo
sistema hanno una sezione pari a 1/3 rispetto all’altro sistema, quindi si
ha un risparmio di materiale.
In alternata (sia monofase che trifase), è più facile effettuare operazioni
di apertura del circuito (ad esempio con interruttori) perchè la corrente
passa spontaneamente per lo zero: questo favorisce il processo di
estinzione dell’arco elettrico che si forma tra i contatti che si
allontanano, senza strapparlo, quindi senza determinare sovratensioni
sul sistema alimentato.
Nella distribuzione interna in BT per sistemi trifasi si usano cinque
conduttori, tre fasi, il neutro e il conduttore di protezione (PE): quando
le sezioni sono consistenti, si può, per carico simmetrico nelle tensioni
ed equilibrato nelle correnti, ridurre la sezione per il conduttore di
neutro, questo comporta dei benefici sul costo della distribuzione.
Nella distribuzione per usi domestici o similari, ma anche nella
distribuzione interna a livello industriale, il sistema a quattro fili, nel
confronto con il monofase, rende indipendenti le utenze finali tra di loro,
poiché in forma ciclica si possono collegare a fasi diverse.
Ripasso del concetto di impedenza elettrica ed il triangolo delle potenze (caso
monofase)
L’impedenza è un operatore vettoriale (quindi una grandezza complessa, non una grandezza
variabile sinusoidalmente nel tempo) definito dalla formula inversa della legge di Ohm
generalizzata:
L'impedenza riassume la resistenza e la reattanza complessive di un ramo, detta f la
frequenza ed = 2Pf è la pulsazione della tensione alternata sinusoidale applicata al ramo,
si ha:
Il modulo dell'impedenza |Z| vale ovviamente:
mentre il suo argomento vale:
e tale argomento coincide con lo sfasamento tra la tensione
applicata all'impedenza e la
corrente che percorre l'impedenza.
Le potenze che riguardano l'impedenza sono:
potenza attiva :
2
P = V·I·cos( V,I) = R·I [W]
(attenzione: i pedici V,I indicano che lo sfasamento f è
l’angolo di sfasamento fra la tensione V e la corrente I)
potenza reattiva, da considerarsi positiva se induttiva, negativa se capacitiva:
2
Q = V·I·sen( V,I) = (XL - XC)·I [VAR]
modulo potenza apparente, che riassume le prime due :
potenza della apparente complessa (
è il complesso coniugato di
):
Le tre potenze di cui sopra si possono riassumere nel seguente triangolo delle potenze:
per il quale valgono le seguenti relazioni:
DEFINIZIONI
Tensione di fase:
d.d.p. Ef esistente fra gli estremi di un singola fase generatrice,
oppure d.d.p. Uf di una singola impedenza utilizzatrice.
Tensione concatenata o tensione di linea EL , UL :
d.d.p. fra due fili della linea di alimentazione. Si determinano dalle d.d.p.
Quando non è indicato il pedice, si intende la tensione concatenata.
Il vettore d.d.p. ha la punta della freccia diretta per convenzione verso il punto
a potenziale maggiore (il vettore quindi parte dal punto a potenziale minore: ad
esempio U12 ha la freccia diretta verso il livello elettrico "1").
Ovviamente il vettore
è opposto rispetto a U12.
Sistema simmetrico trifase:
le tensioni di ogni singola fase del generatore hanno stesso modulo e sono sfasate di
360°/3 = 120°.
In questo anche la terna delle tensioni concatenate è simmetrica.
Corrente di fase: è la corrente che percorre la fase generatrice o utilizzatrice.
Corrente di linea: è la corrente che percorre la linea di alimentazione.
Carico trifase equilibrato: le tre impedenze di fase sono identiche, con stesso modulo
e stessa fase.
Collegamento a stella :
la corrente di fase coincide con la corrente di linea;
la tensione di linea è
Collegamento a triangolo :
la corrente di linea è maggiore rispetto alla corrente di fase, se il carico è
equilibrato si ha
la tensione di fase coincide con la tensione di linea , ossia Uf = UL
Sistema trifase con neutro :
dai morsetti del generatore escono tre fili di linea che si collegano ai tre
morsetti del carico trifase; inoltre
dal centro stella del generatore parte il filo neutro che va al centro stella del
carico trifase di arrivo.
Quando il carico trifase allacciato è equilibrato il conduttore neutro non è percorso da
corrente
Il conduttore neutro mantiene sempre immutato il modulo delle tensioni di fase,
anche con carichi squilibrati e vale sempre la relazione
La presenza di uno squilibrio del carico determina il passaggio di una
corrente nel conduttore neutro, nel quale si richiude la somma vettoriale delle
correnti dei tre fili di linea. Si può dire che in tal caso il neutro costituisce il filo
di ritorno della somma delle correnti dei fili di linea (somma algebrica dei loro
valori istantanei o somma vettoriale dei vettori ad esse associate).
Sistema trifase senza neutro:
Se il carico trifase è equilibrato vale ancora la relazione fra tensioni di
fase e concatenate:
Se il carico trifase è squilibrato le cose si complicano: le tensioni di fase
possono assumere valori imprevisti e anche pericolosi per le fasi utilizzatrici.
Terne simmetriche di tensioni stellate e concatenate
Il sistema di distribuzione trifase si compone di tre fili di linea (fili 1, 2, 3) sempre presenti e di un
filo neutro (filo 0) che può anche mancare.
Le tensioni presenti tra ciascun filo di linea ed il neutro sono chiamate tensioni stellate (o tensioni di
fase). Esse costituiscono una terna isofrequenziale di tensioni sinusoidali sfasate di 120° l'una
rispetto all'altra e di uguale valore efficace:
Il posizionamento della prima tensione stellata
è del tutto arbitrario, ovviamente da tale scelta
dipendono poi le posizioni delle altre tensioni (è conveniente utilizzare sempre lo stesso
posizionamento, che può essere quello di figura).
Le tensioni presenti tra due fili di linea sono chiamate tensioni concatenate (o tensioni di linea).
Esse risultano essere la differenza tra due tensioni stellate e si dimostra facilmente che costituiscono
una terna isofrequenziale di tensioni sinusoidali sfasate di 120° l'una rispetto all'altra e di uguale
valore efficace. Il valore di tali tensioni è
volte il valore delle tensioni stellate e la terna
concatenata è in anticipo di 30° sulla terna stellata:
In un impianto trifase, la tensione nominale è sempre quella concatenata.
Nella distribuzione finale in bassa tensione i valori convenzionali sono rispettivamente di 380 [V]
per la tensione concatenata e di:
per quella stellata alla frequenza industriale di 50 [Hz] cui corrisponde la pulsazione di 314,2
[rad/s].
Sistemi simmetrici ed equilibrati
Sono i sistemi trifasi nei quali sia le tensioni concatenate (e quindi anche quelle stellate) che le
correnti di linea
costituiscono una terna simmetrica di grandezze alternate sinusoidali.
Perché le correnti di linea costituiscano una terna simmetrica è necessario che le tre impedenze di
carico siano tra di loro uguali. Si parla di sistemi simmetrici nelle tensioni ed equilibrati nelle
correnti (o nel carico).
Sistema simmetrico a tre fili e carico equilibrato a triangolo
Su ciascuna impedenza del carico:
è applicata la tensione concatenata, quindi in ciascuna impedenza circolerà una corrente, chiamata
corrente di fase di modulo pari a:
sfasata dell'angolo rispetto alla corrispondente tensione concatenata (la figura è riferita al caso di
carico Ohmico-induttivo nel quale la corrente di fase è in ritardo rispetto alla tensione concatenata
di un angolo pari all'argomento dell'impedenza). Ovviamente le tre correnti di fase
costituiranno una terna trifase simmetrica di vettori.
Le correnti di linea si trovano come differenza vettoriale tra quelle di fase:
ed è facile verificare che avranno eguale modulo pari a:
e saranno sfasate rispetto alle corrispondenti tensioni stellate di un angolo uguale all'argomento
dell'impedenza di carico. Anche le tre correnti di linea costituiranno una terna trifase simmetrica di
vettori.
Per quanto riguarda le potenze, si può scrivere:
dove la potenza reattiva sarà negativa nel caso di carico Ohmico-capacitivo essendo negativa la
reattanza capacitiva.
E' anche possibile calcolare le potenze nel seguente modo:
ed in effetti sono proprio queste le espressioni più spesso impiegate per il calcolo delle potenze nei
sistemi trifasi simmetrici ed equilibrati e, come vedremo, rimangono invariate qualunque sia il
collegamento del carico.
Sistema simmetrico a quattro fili e carico equilibrato a stella
A causa del collegamento del centro stella 0' al filo neutro 0 si ha che ciascuna impedenza di fase:
è sottoposta alla corrispondente tensione stellata. La corrente in ciascuna impedenza di fase è la
stessa di linea ed ha la stessa intensità per tutte e tre le fasi, più precisamente:
In ciascuna fase la corrente è sfasata rispetto alla tensione stellata di un angolo uguale all'argomento
dell'impedenza (supposta Ohmico-induttiva in figura) e le tre correnti di linea
costituiranno una terna simmetrica sfasata rispetto alla terna delle tensioni stellate
dell'angolo =
Ovviamente sarà:
così che, applicando il primo principio di Kirchhoff al centro della stella, risulterà per il neutro:
.
Per quanto riguarda le potenze, si può scrivere:
dove la potenza reattiva sarà negativa nel caso di carico Ohmico-capacitivo essendo negativa la
reattanza capacitiva.
E' anche possibile calcolare le potenze nel seguente modo:
Sistema simmetrico a tre fili e carico equilibrato a stella
Considerando che nel collegamento del centro stella al neutro non circola alcuna corrente è
possibile togliere il collegamento stesso senza alterare il regime elettrico della rete. Si conclude così
che il sistema a tre fili col carico equilibrato a stella è del tutto analogo al caso dei quattro fili sopra
visto. Risulta inoltre che la tensione presente ai capi di ciascuna impedenza di fase di una stella
equilibrata vale sempre:
indipendentemente dal valore dell'impedenza.
Da quanto sopra esposto si ha che teoricamente è del tutto indifferente realizzare o meno il
collegamento del centro di una stella equilibrata al filo neutro, nella pratica tale collegamento può
invece essere molto importante. Infatti se si verifica un guasto qualsiasi in una delle tre impedenze
della stella si avrà che cambierà il valore dell'impedenza stessa così che la stella diverrà squilibrata:
nelle nuove condizioni il comportamento dell'impianto è sostanzialmente diverso nel caso di
collegamento del centro al neutro rispetto al caso nel quale il collegamento manchi. Se vi è il
collegamento al neutro la tensione ai capi di ciascuna fase rimarrà la stessa nonostante il guasto, se
manca il collegamento la tensione ai capi delle tre fasi cambierà dopo il guasto e potrà assumere
valori anche molto maggiori di quelli che si avevano prima del guasto (tutto questo sarà chiarito nei
seguenti paragrafi).
Come si vedrà, le potenze possono anche essere determinate tramite l'inserzione di wattmetri sui fili
di linea. Nel caso di sistemi simmetrici ed equilibrati, siano essi col carico a stella che a triangolo, si
usa lo schema Aron sia per la potenza attiva che per la reattiva.
Osservazione: nei sistemi trifasi simmetrici ed equilibrati, siano essi col carico a stella che a
triangolo, per sfasamento si intende l'angolo misurato tra la terna delle tensioni stellate e la terna
delle correnti di linea. Tale angolo coincide con l'argomento dell'impedenza del carico.
Sistemi simmetrici e squilibrati
Sono i sistemi trifasi nei quali solo le tensioni concatenate (e quindi le stellate) costituiscono una
terna simmetrica di vettori, le correnti di linea e quella nel neutro (se presente) soddisfano invece
unicamente il primo principio di Kirchhoff:
Sistema simmetrico a tre fili e carico squilibrato a triangolo
Con riferimento allo schema si calcolano per prima cosa le correnti di fase:
Quindi, applicando Kirchhoff, si calcolano le correnti di linea:
Le tre correnti dovranno soddisfare la condizione
.
Per quanto riguarda le potenze:
Sistema simmetrico a quattro fili e carico squilibrato a stella
Con riferimento allo schema si calcolano subito le correnti di linea:
mentre la corrente nel neutro varrà:
Per quanto riguarda le potenze:
Sistema simmetrico a tre fili e carico squilibrato a stella
Mancando il collegamento del centro stella 0' al neutro 0 non si può più dire che la tensione
applicata a ciascuna impedenza coincida con la tensione stellata. In effetti le tensioni applicate alle
singole fasi dipendono dal valore delle impedenze e si possono determinare dopo avere determinato
lo spostamento del centro stella
della stella ed il neutro.
[V], ovvero la differenza di potenziale esistente tra il centro
Tutto questo è possibile applicando il principio di Millman alla rete equivalente al sistema trifase:
La tensione applicata a ciascuna impedenza varrà:
La corrente in ciascuna fase (che corrisponde alla corrente di linea), varrà:
Le tre correnti dovranno soddisfare la condizione
.
Per quanto riguarda le potenze valgono le stesse equazioni del caso precedente.
Come si vedrà, le potenze possono anche essere determinate tramite l'inserzione di wattmetri sui fili
di linea. Nel caso di sistemi simmetrici e squilibrati, siano essi col carico a stella che a triangolo, per
la potenza attiva si usa lo schema Aron, per la potenza reattiva si usa lo schema Righi o lo schema
Barbagelata.
Si definisce f.d.p. globale:
Osservazione: nei sistemi trifasi simmetrici e squilibrati, siano essi col carico a stella che a
triangolo, per sfasamento globale G si intende l'angolo del quale è necessario ruotare rigidamente
la terna (non simmetrica) dei vettori rappresentanti le correnti di linea al fine di rendere massima la
potenza attiva dell'intero sistema.
Casi particolari
Nel sistema a tre fili con carico a stella (o a quattro fili ma senza il collegamento del centro stella al
neutro), se una delle fasi è in cortocircuito ideale accade che il centro della stella assume il
potenziale del filo di linea al quale la fase stessa è collegata. In queste condizioni non è possibile
applicare la formula di Millman (perché due frazioni avrebbero denominatore nullo), si deve quindi
risolvere applicando convenientemente le note leggi dell'elettrotecnica.
Se il carico è a triangolo oppure a stella col collegamento del centro al neutro, la condizione di una
fase in cortocircuito ideale produce un assurdo e,quindi, non è studiabile (la corrente nella fase in
cortocircuito tende ad essere infinitamente grande).
L'interruzione di una fase, pur producendo sempre uno squilibrio nel sistema, conduce a casi
risolvibili applicando quanto esposto nei paragrafi precedenti.
Teorema di Boucherot
In un sistema elettrico in regime sinusoidale costituito da più utilizzatori si può dire che:
a) la potenza attiva totale è data dalla somma aritmetica delle singole potenze attive:
b) la potenza reattiva totale è data dalla somma algebrica delle singole potenze reattive assunte
positive se induttive, negative se capacitive:
c) la potenza apparente complessa totale è data dalla somma vettoriale delle singole potenze
apparenti complesse, in ogni caso il modulo della potenza apparente totale si può più
convenientemente determinare con: